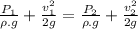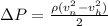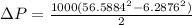Question

What is the pressure drop due to the bernoulli effect as water goes into a 3.00-cm-diameter nozzle from a 9.00-cm-diameter fire hose while carrying a flow of 40.0 l/s?

Answer 1

`\Delta P=1581357.92\ Pa`

Step-by-step explanation:

Given:

• diameter of hose pipe,
  `D=0.09\ m`

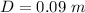
• diameter of nozzle,
  `d=0.03\ m`

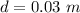
• volume flow rate,
  `\dot{V}=40\ L.s^(-1)=0.04\ m^3.s^(-1)`

Now, flow velocity in hose:

`v_h=(\dot V)/(\pi.D^2/ 4)`

`v_h=(0.04* 4)/(\pi* 0.09^2)`

`v_h=6.2876\ m.s^(-1)`

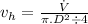
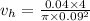
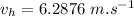
Now, flow velocity in nozzle:

`v_n=(\dot V)/(\pi.d^2/ 4)`

`v_n=(0.04* 4)/(\pi* 0.03^2)`

`v_n=56.5884\ m.s^(-1)`

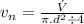
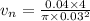
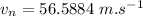
We know the Bernoulli's equation:

`(P_1)/(\rho.g)+(v_1^2)/(2g)+Z_1=(P_2)/(\rho.g)+(v_2^2)/(2g)+Z_2`

when the two points are at same height then the eq. becomes

`(P_1)/(\rho.g)+(v_1^2)/(2g)=(P_2)/(\rho.g)+(v_2^2)/(2g)`

`\Delta P=(\rho(v_n^2-v_h^2))/(2)`

`\Delta P=(1000(56.5884^2-6.2876^2))/(2)`

`\Delta P=1581357.92\ Pa`