Question

What type of exponential function is f(x)=0.6(2.4)^x ?

What is the function's percent rate of change?


Select from the drop-down menus to correctly complete each statement.

The function is an exponential (growth,decay) function.

The percent rate of change of the function is (240,140,60,40) %.

Answer 1

The function is an exponential GROWTH function.

The percent rate of change of the function is 140%.

Explanation:

Answer 2

The function is of an exponential growth type

Rate of change is 240%

Explanation:

Exponential Function

The expression of an exponential function is

`f(x)=c.a^(bx)`

For a,b,c constants.

1.

The function will be of an exponential growth type if, when x increases, f increases. That behavior comes from the combination of the three constants a,b,c. The best approach to find that out is by taking the first derivative

`f'(x)=b.c.lna.a^(bx)`

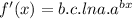
Since
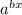`a^(bx)` is always positive, the product of b.c.lna must be positive to make f increasing. For example, if a>1 and both b and c are of the same sign, f increases for all x. If 0<a<1, then, since lna<0, the product b.c must be negative, i.e. both should have different signs

The function is expressed as

`f(x)=0.6\ 2.4^x`

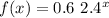
we can see a>1, b and c are positive, so the function is of an exponential growth type.

2.

Talking about rates change of real functions takes us to the derivative function. We have already seen the derivative is dependent on all three constants and also of the value of x, so it cannot be predicted as a fixed percentage.

Now, if we picture the function as the general term of a sequence, where x can only take natural values, we can say

`\displaystyle (0.6(2.4)^(x+1))/(0.6(2.4)^(x))=2.4`

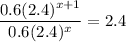
Each term is obtained as the previous term by 2.4. It's accurate to say the rate of change is 240%