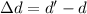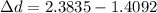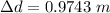Question

A catfish is spotted at the bottom of a creek. The depth of the water is 2 m. A hunter (with no knowledge of optics) fires a rifle shot, directly aimed at the catfish. The bullet strikes the water at an angle of 40° to the water. Assume that the bullet is not deflected by the air/water interface, what is the distance from the bullet hole at the bottom of the creek to the catfish? Water: n=1.33. (Answer should be 0.97 m)

Answer 1

`\Delta d=0.9743\ m`

Step-by-step explanation:

Given:

• depth of fish,
  `h=2\ m`

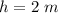
• angle of incidence,
  `\angle i=90-40=50^(\circ)`

• refractive index of water,
  `n=1.33`

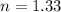
Apparent distance from the normal projection at the bottom of entrance at air-water surface to the fish:

`d'=h.tan\ \theta`

`d'=2* tan\ 50`

`d'=2.3835\ m`

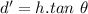
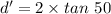
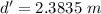
Now according to Snell's Law:

`n=(sin\ i)/(sin\ r)`

`1.33=(sin\ 50)/(sin\ r)`

`\angle r=35.168^(\circ)`

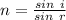
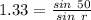
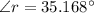
Now the actual distance of the fish from the bottom surface at the normal:

`d=h.tan\ \theta`

`d=2* tan\ 35.168`

`d=1.4092\ m`

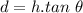
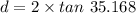
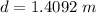
Now distance between bullet hole and fish:

`\Delta d=d'-d`

`\Delta d=2.3835-1.4092`

`\Delta d=0.9743\ m`