To solve this problem it is necessary to apply the equations related to the conservation of momentum.
This definition can be expressed as
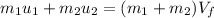
Where
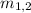 = Mass of each object
= Mass of each object
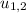 = Initial Velocity of each object
= Initial Velocity of each object
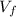 = Final velocity
= Final velocity
Rearranging the equation to find the final velocity we have,
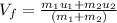
Our values are given as
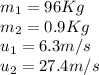
Replacing we have,
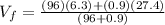
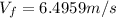
Therefore the final velocity is 6.5m/s