1 Answer

Prasob · Answer 1 · 2020-03-21T02:30:34+0000

The equation represents a line that includes the points(2,-2) and (6,-4) is
y=(-1)/(2) x-1

Given that two points are (2, -2) and (6, -4)

We have to find the equation of line containing these points

The equation of line with points
(x_1, y_1) and
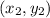(x_2, y_2) is given as:

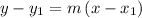
$y-y_(1)=m\left(x-x_(1)\right)$

Where "m" is the slope of line

The slope of line "m" is given as:

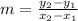
m=(y_(2)-y_(1))/(x_(2)-x_(1))

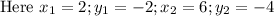
$\text {Here } x_(1)=2 ; y_(1)=-2 ; x_(2)=6 ; y_(2)=-4$

Substituting the values in slope formula we get,

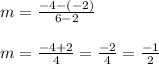
$\begin{array}{l}{m=(-4-(-2))/(6-2)} \\\\ {m=(-4+2)/(4)=(-2)/(4)=(-1)/(2)}\end{array}$

The required equation is given as:

Substitute "m" value in equation of line formula

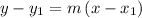
$y-y_(1)=m\left(x-x_(1)\right)$

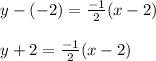
$\begin{array}{l}{y-(-2)=(-1)/(2)(x-2)} \\\\ {y+2=(-1)/(2)(x-2)}\end{array}$

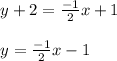
$\begin{array}{l}{y+2=(-1)/(2) x+1} \\\\ {y=(-1)/(2) x-1}\end{array}$

Thus the equation of line is found out

Please log in or register to add a comment.