The equation represents a line that includes the points(2,-2) and (6,-4) is
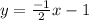
Solution:
Given that two points are (2, -2) and (6, -4)
We have to find the equation of line containing these points
The equation of line with points
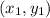 and
and
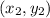 is given as:
is given as:
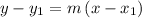
Where "m" is the slope of line
The slope of line "m" is given as:
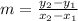
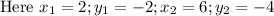
Substituting the values in slope formula we get,
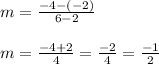
The required equation is given as:
Substitute "m" value in equation of line formula
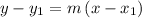
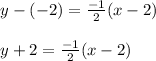
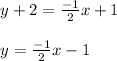
Thus the equation of line is found out