Answer: The required answers are
(a) NOT orthogonal.
(b) NOT orthonormal.
(c) Not a basis,
Step-by-step explanation: We are given to consider the vectors {(1, −6, 3, 2), (1, 2, 0, 6)}.
(a) We are to determine whether the set of vectors in
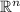 is orthogonal.
is orthogonal.
(b) If the set is orthogonal, then to determine whether it is also orthonormal.
(c) To determine whether the set is a basis for
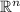 .
.
We know that
any two vectors u and v are orthogonal, if their dot product u.v is zero.
The dot product of (1, −6, 3, 2) and (1, 2, 0, 6) is given by

So, the given set is not orthogonal.
Since the vectors are not orthogonal, they cannot be orthonormal.
To be a basis of
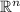 , the set must contain n vectors.
, the set must contain n vectors.
Here, we are dealing with
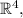 and the set contains only 2 vectors.
and the set contains only 2 vectors.
So, the given set cannot be a basis.