Answer:

Explanation:
We are given that
Total length of fence=180 m
Let length of rectangular field=x
Width of rectangular field=y
According to question
Length of fencing=x+2y
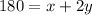
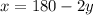
Area of rectangular field=
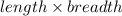
Area of rectangular field=
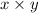
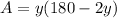
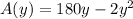
Differentiate w.r.t y
A'(y)=180-4y
A'(y)=0
180-4y=0
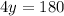
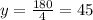
Again differentiate w.r.t y
A''(y)=-4<0
Areas of rectangular field is minimum at y=45
Substitute the value then, we get
x=180-2(45)=90
Dimensions of rectangular field are 90 m by 45 m