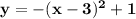Question

What is the equation of the graph below? A graph shows a parabola that opens down with a vertex at three comma one. y = − (x − 3)2 + 1 y = − (x + 1)2 + 4 y = (x + 1)2 − 4 y = (x − 4)2 + 1

Answer 1

It's A.

Explanation:

I got it right on the test. The expert above explained it in pure detail.

Answer 2

The option must be:

• 
  `\mathbf{y=-(x-3)^(2)+1}`
• 
  `\mathbf{y=-(x+1)^(2)+4}`
• 
  `\mathbf{y=(x+1)^(2)-4}`
• 
  `\mathbf{y=-(x-4)^(2)+1}`

Answer:

`\mathbf{y=-(x-3)^(2)+1}`

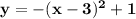
Explanation:

There are generally two forms in which quadratic equation is represented:

1. 
   `\mathrm{y=ax^(2)+bx+c}`
2. 
   `\mathrm{y=a(x-h)^(2)+k}`

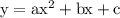
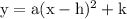
The options here are given in the second form, so by interpreting the second form in graphical form will give the the answer.

In second form 'h' and 'k' are the x-coordinate and y-coordinate respectively of the vertex of parabola.

In the given graph the coordinates of vertex is (3 , 1).

So h = 3 and k = 1.

In the second form 'a' decide the direction of opening of parabola, if a is greater than zero than the opening is upward and if a is less than zero than opening of parabola is downwards.

In the given graph the parabola opens downward so the value of a is -1.

a = -1

Therefore the final equation of parabola is as follows:

`\mathbf{y=-(x-3)^(2)+1}`