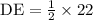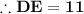Question

Can someone help me with this asap

Answer 1

`\mathbf{DE=11}`

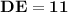
Explanation:

given AD = DB , means D is the midpoint of AB

given AE = EC , means E is the midpoint of AC

MID POINT THEOREM

In a triangle ABC, if D and E is the midpoint of side AB and AC respectively.

Then DE is parallel to BC and length of DE is half of length of BC.

`\mathbf{DE=(1)/(2)BC}`

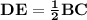
BC = 22 (given in the question)

`\mathrm{DE=(1)/(2)*22}`

`\therefore\mathbf{DE=11}`