Question

The area of two similar octagons are 4 m2 and 25 m2. What is the scale factor of their side lengths

Answer 1

The scale factor of the sides of the Octagon is 2:5

Explanation:

Both these octagons can be considered as the combination of 8 similar triangles joined edge to edge.

We know this property of similar triangles, that the ratio of area of similar triangles is proportion to the square of the ratio of sides of the similar triangle.

`Side_(1) ^(2) : Side_(2) ^(2) =Area_(1) : Area _(2)`

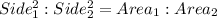
From the above property, we plug in the values

`Side_(1) ^(2) : Side_(2) ^(2) =4: 25`

`Side_(1)  : Side_(2)  =2: 5`

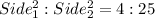
Therefore, the ratio of the sides of the Octagon are 2:5.