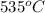Answer : The correct option is, (d)
Explanation :
In this problem we assumed that heat given by the hot body is equal to the heat taken by the cold body.
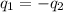
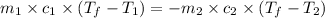
where,
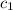 = specific heat of copper =
= specific heat of copper =

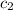 = specific heat of water =
= specific heat of water =
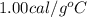
 = mass of copper = 120 g
= mass of copper = 120 g
 = mass of water = 300 g
= mass of water = 300 g
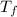 = final temperature of mixture =
= final temperature of mixture =

 = initial temperature of copper = ?
= initial temperature of copper = ?
 = initial temperature of water =
= initial temperature of water =
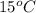
Now put all the given values in the above formula, we get:
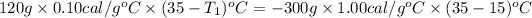
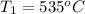
Therefore, the temperature of the kiln was,