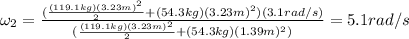Answer:
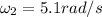
Step-by-step explanation:
Since there is no friction angular momentum is conserved. The formula for angular momentum thet will be useful in this case is
 . If we call 1 the situation when the student is at the rim and 2 the situation when the student is at
. If we call 1 the situation when the student is at the rim and 2 the situation when the student is at
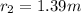 from the center, then we have:
from the center, then we have:
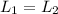
Or:
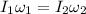
And we want to calculate:
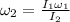
The total moment of inertia will be the sum of the moment of intertia of the disk of mass
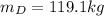 and radius
and radius
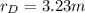 , which is
, which is
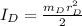 , and the moment of intertia of the student of mass
, and the moment of intertia of the student of mass
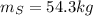 at position
at position
 (which will be
(which will be
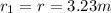 or
or
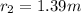 ) will be
) will be
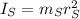 , so we will have:
, so we will have:
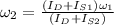
or:
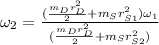
which for our values is: