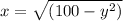Question

Which equation represents the value of x? x=100−y2−−−−−−−√ x=10+y2 x=10−y x=y2+100−−−−−−−√ Right triangle A B C with angle B as the right angle. A C is equal to 10. B C is equal to y. A B is equal to x.

Answer 1

Therefore the required value of x,

`x=\sqrt{(100-y^(2))}`

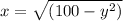
Explanation:

Given:

ΔBC is a Right Angle Triangle at ∠ B = 90°

As ∠ B = 90° , AC will be the Hypotenuse

AC = 10 = Hypotenuse

BC = y = Longer leg ( say )

AB = x = Shorter leg ( say )

To Find :

x = ?

Solution:

In Right Angle Triangle Δ ABC , By Pythagoras Theorem we get

`(\textrm{Hypotenuse})^(2) = (\textrm{Shorter leg})^(2)+(\textrm{Longer leg})^(2)`

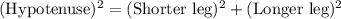
Substituting the given values we get

`10^(2)= x^(2)+y^(2) \\\\x^(2)=100-y^(2) \\\\\textrm{square rooting on both the side we get}\\\\x=\sqrt{(100-y^(2))}\\\therefore x=\sqrt{(100-y^(2))}\ \textrm{ which is the required value of x}`

Therefore the required value of x,

`x=\sqrt{(100-y^(2))}`