Answer:
Option C is correct.
Explanation:
We have to simplify the product of
(StartRoot 6 x squared EndRoot + 4 StartRoot 8 x cubed EndRoot) (StartRoot 9 x EndRoot minus x StartRoot 5 x Superscript 5 Baseline)
=
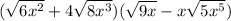
=
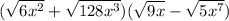
=
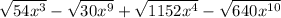
=
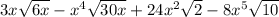
= 3 x StartRoot 6 x EndRoot minus x Superscript 4 Baseline StartRoot 30 x EndRoot + 24 x squared StartRoot 2 EndRoot minus 8 x Superscript 5 Baseline StartRoot 10 EndRoot
Therefore, option C is correct. (Answer)