Question

A gumball has a diameter that is 66 mm. The diameter of the gumball's spherical hollow core is 58 mm. What is the volume of the gumball if you do not include its hollow core? Use 3.14 for π on your calculator. Round your answer to the nearest tenth if necessary.

Answer 1

Volume of gumball without including its hollow core is 48347.6 cubic mm.

Explanation:

Given:

Diameter of Gumball = 66 mm

Since radius is half of diameter.

Radius of gumball =
`(diameter)/(2)=(66)/(2) =33 \ mm`

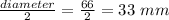
Now We will first find the Volume of Gumball.

To find the Volume of Gumball we will use volume of sphere which is given as;

Volume of Sphere =
`(4)/(3)\pi r^3`

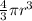
Now Volume of Gumball =
`(4)/(3)*3.14 * (33)^3 = 150456.24 \ mm^3`

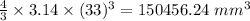
Also Given

Diameter of gumball's spherical hollow core = 58 mm

Since radius is half of diameter.

Radius of gumball's spherical hollow core =
`(diameter)/(2)=(58)/(2) =29 \ mm`

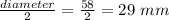
Now We will find the Volume of gumball's spherical hollow core.

Volume of Sphere =
`(4)/(3)\pi r^3`

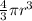
So Volume of gumball's spherical hollow core =
`(4)/(3)*3.14 * (29)^3 = 102108.61 \ mm^3`

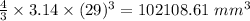
Now We need to find volume of the gumball without including its hollow core.

So, To find volume of the gumball without including its hollow core we would Subtract Volume of gumball spherical hollow core from Volume of Gumball.

volume of the gumball without including its hollow core = Volume of Gumball - Volume of gumball's spherical hollow core =
`150456.24\ mm^3 - 102108.61\ mm^3 = 48347.63\ mm^3`

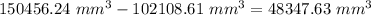
Rounding to nearest tenth we get;

volume of the gumball without including its hollow core =
`48347.6\ mm^3`

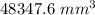
Hence Volume of gumball without including its hollow core is 48347.6 cubic mm.