Question

A landscaping company charges customers for lawn care based on the area of their yards. Mr. Jones was charged $52 for his yard, which is 40 feet by 65 feet. If a neighbor’s yard is 50 feet by 80 feet, what would the neighbor be charged based on how much Mr. Jones was charged?

Answer 1

Here is the simple version:

- Your answer is $80

Explanation:

Mr. Jones was charged $52 for his yard, which is 40 feet by 65 feet.

So if the neighbor's was 50 feet by 80 feet, then

40 + 10 = 50

and 80-65=25

(This represents Mr. Jones and his neighbor's feet)

Okay, then you add 50+25=75 to get the amount his neighbor would be charged for his yard.

Answer 2

Landscaping Company will charge $80 for Neighbor yard.

Explanation:

Given:

Charges of Mr. Jones = $52

Length of Mr. Jones yard = 65 feet

Width of Mr. Jones yard = 40 feet

Now we will find the area of Mr. Jones yard.

Yard is basically in rectangular form.

Hence we can;

Area of yard is equal to product of length of the yard and width of the yard.

Framing in equation we get;

Area of Mr. Jones Yard =
`40* 65 = 2600\ ft^2`

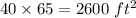
Now Mr. Jones was charged $52 for a yard having Area 2600 sq. ft.

So we will find the per sq. ft charge applied by the company.

Per sq. ft charge will be equal to Charges of Mr. Jones divided by Area of Mr. Jones Yard.

Framing in equation form we get;

Per sq. ft charge =
`(52)/(2600) = \$0.02`

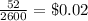
Hence the Landscaping company charge Mr. Jones at $0.02 per sq.ft.

Now Given:

Length of Neighbor yard = 80 ft.

Width of Neighbor yard = 50 ft.

We need to find the Charges on Neighbor based on charges applied on Mr. Jones.

First we will find the Area of Neighbors yard we get;

Area of Neighbors yard =
`80 *50 = 4000\ ft^2`

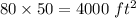
Charges of Neighbor yard will be equal to charges Landscaping company for per sq. ft multiplied by area of Neighbors yard.

Framing in equation form we get;

Charges of Neighbor yard =
`0.02* 4000 = \$80`

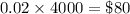
Hence Landscaping Company will charge $80 for Neighbor yard.