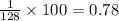Question

What percentage of a radioactive substance remains after 7.00 half-lives have elapsed?0.391%1.56%3.12%0.78%

Answer 1

Percentage of a radioactive substance remains after 7.00 half-lives have elapsed is 0.78%.

Step-by-step explanation:

Formula used :

`A=(A_o)/(2^n)`

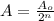
where,

A = amount of reactant left after n-half lives

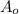`A_o` = Initial amount of the reactant

n = number of half lives

We have:

n = 7.00

`A=(A_o)/(2^7)`

`(A)/(A_o)=(1)/(128)`

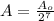
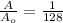
Percentage of a radioactive substance remains after 7.00 half-lives have elapsed:

=
`(1)/(128)* 100=0.78%`