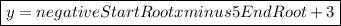Question

Which function has a domain of x greater-than-or-equal-to 5and a range of y less-than-or-equal-to 3?

A. y = StartRoot x minus 5 EndRoot + 3
B. y = StartRoot x + 5 EndRoot minus 3
C. y = negative StartRoot x minus 5 EndRoot + 3
D. y = negative StartRoot x + 5 EndRoot minus 3

Answer 1

C. y = negative StartRoot x minus 5 EndRoot + 3

Explanation:

Answer 2

Option C.

y = negative StartRoot x minus 5 EndRoot + 3

Explanation:

Domain and Range of Functions

Let's consider a function y=f(x) where x is a set of values such as f exists. All the values of x are called the domain of f. Similarly, f takes a set of values when x takes values in its domain. All the values f could take is its range

We know the domain and range of f are, respectively

`x\geq 5,\ y\leq 3`

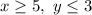
Since all the options contain a square root, we already know the domain will be restricted by the argument of a square root, that is, it must be non-negative. From the given domain, we construct the argument of the square root

`x\geq 5`

`x-5\geq 0`

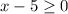
It corresponds to the argument of a square root that must be non-negative. So our function must contain

`√(x-5)`

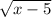
Now about the range, the square root is assumed as positive or zero, and the range is restricted as less or equal to zero, so we operate the inequality for y

`y\leq 3\ =>\ 0\leq 3-y\ =>\ 3-y\geq 0`

Now we can safely say

`3-y=√(x-5)`

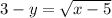
Or equivalently

`y=3-√(x-5)`

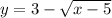
This corresponds to the option C. written as

`\boxed{y = negative StartRoot x minus 5 EndRoot + 3}`