Question

Two ropes apply a force to a boat. The first is 700 N in the positive x direction and 300 N in the positive y direction. In At what angle (clockwise from the positive x-axis) must a third rope tension be applied in order to keep the boat at rest?

Answer 1

`\theta=156.81^(\circ)`

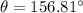
Step-by-step explanation:

It is given that,

Force due to rope 1,
`F_x=700\ N`

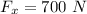
Force due to rope 2,
`F_y=300\ N`

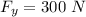
Let
`\theta` is the angle must a third rope tension be applied in order to keep the boat at rest. It can be given by :

`tan\theta=(F_y)/(F_x)`

`tan\theta=(300)/(700)`

`\theta=23.19^(\circ)`

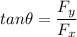
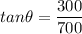
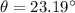
The angle clockwise from the positive x-axis will be equal to,

`\theta=180-23.19`

`\theta=156.81^(\circ)`

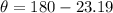
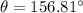
So, the angle must a third rope tension be applied in order to keep the boat at rest is 156.81 degrees. Hence, this is the required solution.