Answer:
The graph in the attached figure
Explanation:
we have
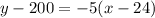
This is the equation of the line in point slope form
where
the slope is
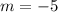
the point is
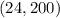
To graph the line i need two points
From the point (24,200) use the slope to find your next point
The slope is -5, so you will rise 5 (down) and run 1 (to the right).
The next point is (24+1,200-5) ----> (25,195)
Plot the points (24,200) and (25,195), join and graph the line
To better understand the problem find the intercepts
For x=0
 --->
--->
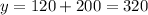
The y-intercept is (0,320)
For y=0
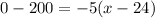 --->
--->
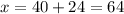
The x-intercept is (64,0)
The graph in the attached figure