Question

Find the distance between the points (0,-2) and (-8,-8)

Answer 1

Distance between the points = 10 units

Explanation:

Given points:

(0,-2) and (-8,-8)

To find the distance between the two points.

Solution:

Applying distance formula to find the distance between the points.

For points
`(x_1,y_1)` and
`(x_2,y_2)` the distance is given as:

`d=√((x_2-x_1)^2+(y_2-y_1)^2)`

Plugging in the given points in the formula.

`d=√((-8-0)^2+(-8-(-2))^2)`

`d=√((-8)^2+(-8+2))^2)`

`d=√((-8)^2+(-6)^2)`

`d=√(64+36)`

`d=√(100)`

`d=\pm10`

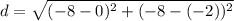
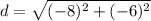
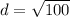
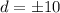
Since distance is always positive. So
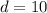`d=10` units.