Answer:
The closest approximate solution to the system of equations is
(–5, –5.9)
Explanation:
we have
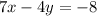 ----> equation A
----> equation A
 ----> equation B
----> equation B
Solve the system by substitution
substitute equation B in equation A
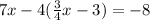
solve for x
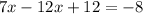
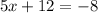
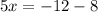

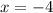
Find the value of y
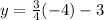
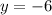
The solution is the point (-4,-6)
Note: The whole procedure to solve the equation system was done for didactic purposes, since the problem is telling me that the point (-4,-6) is common for both lines
therefore
The closest approximate solution to the system of equations is
(–5, –5.9)