Question

What is the pressure drop (due to the Bernoulli Effect) as water goes into a 3.00 cm diameter nozzle from a 9.00 cm diameter fire hose while carrying a flow of 40.0 L/s? (b) To what maximum height above the nozzle can this water rise? (The actual height will be significantly smaller due to air resistance.)

Answer 1

1581357.68216 Pa

163.21352 m

Step-by-step explanation:

A = Area =
`\pi r^2`

v = Velocity

1 denotes inlet

2 denotes exit

`\rho` = Density of water = 1000 kg/m³

Flow rate is given by

`Q=A_1v_1\\\Rightarrow v_1=(Q)/(A_1)\\\Rightarrow v_1=(40* 10^(-3))/(\pi 0.045^2)\\\Rightarrow v_1=6.2876\ m/s`

`Q=A_2v_2\\\Rightarrow v_2=(Q)/(A_2)\\\Rightarrow v_2=(40* 10^(-3))/(\pi 0.015^2)\\\Rightarrow v_1=56.58842\ m/s`

From the Bernoulli equation we get

`P_1+(1)/(2)\rho v_1^2=P_2+(1)/(2)\rho v_2^2\\\Rightarrow P_2-P_1=(1)/(2)\rho (v_2^2-v_1^2)\\\Rightarrow \Delta P=(1)/(2)1000 (56.58842^2-6.2876^2)\\\Rightarrow \Delta P=1581357.68216\ Pa`

The pressure drop is 1581357.68216 Pa

From the Bernoulli equation

`P_a+(1)/(2)\rho v_1^2=P_a+(1)/(2)\rho v_2+\rho gh\\\Rightarrow h=((1)/(2)v_1^2)/(g)\\\Rightarrow h=((1)/(2)56.58842^2)/(9.81)\\\Rightarrow h=163.21352\ m`

The height is 163.21352 m

Answer 2

(a) 1581935 Pa

(b) 161.4 m

Step-by-step explanation:

diameter, d = 3 cm

r = 1.5 cm

diameter, d = 9 cm

R = 4.5 cm

Volume per second, V = 40 L/s = 0.04 m^3/s

V = a x v1

0.04 = 3.14 x 0.015 x 0.015 x v1

v1 = 56.6 m/s

Now, 0.04 = 3.14 x 0.045 x 0.045 x v2

v2 = 6.3 m/s

(a) By use of Bernoullie's theorem

`P_(1)+(1)/(2)dv_(1)^(2)=P_(2)+(1)/(2)dv_(2)^(2)`

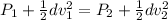
where, d be the density of water

`P_(1)+(1)/(2)* 1000* 56.6* 56.6=P_(2)+(1)/(2)* 1000* 6.3* 6.3`

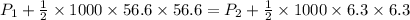
P2 - P1 = 1581935 Pa

(b) Let h be the maximum height

P2 - P1 = x d x g

1581935 = h x 1000 x 9.8

h = 161.4 m