Answer:

Step-by-step explanation:
Given that,
Torque,
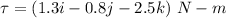
Force,
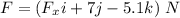
Position vector,
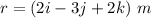
Torque acting on the particle is given by :
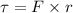
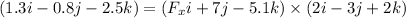
The coefficient of i should be same. So,
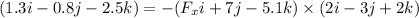
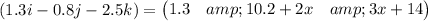
On comparing both sides, we get :

So, the x component of force is 5.5 N. Hence, this is the required solution.