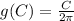Answer:
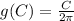
Explanation:
Let r represent the radius of the circle (in cm) and
let C represent the circumference of the circle (in cm).
First solve the equation for 'r' using circumference formula
Circumference of circle formula is
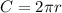
Solve for r, divide both sides by 2pi
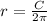
the function g determines the radius of the circle in cm
So we replace 'r' with g(C), where C is the circumference