To solve this problem it is necessary to apply the kinematic equations of motion (vertical in this case) as well as the momentum conservation equations.
For conservation of the moment we have to
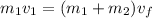
Where
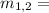 Mass of each object
Mass of each object
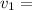 Initial velocity of arrow
Initial velocity of arrow
 = Final Velocity
= Final Velocity
Time in flight for arrow-apple combination is

Where,
h = Max height
g = Gravitational acceleration
Now after the impact arrow-apple combination have horizontal velocity V and it is
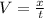
From the previous definition we have that the value of time would be,
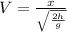
Assuming the son's height is 1.85m, then we should

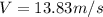
Applying again the conservation equation we can obtain the value of the apple mass as:
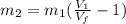
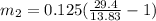
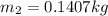

Therefore the mass of the apple was 140.7g