To solve this problem it is necessary to apply the concepts related to Sound Intensity. The unit most used in the logarithmic scale is the decibel and mathematically this is expressed as
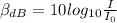
Where,
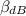 = Sound intensity level in decibels
= Sound intensity level in decibels
I = Acoustic intensity on the linear scale
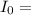 Hearing threshold
Hearing threshold
According to the values, the total intensity is 32 times the linear intensity and the value in decibels is 83dB
So:
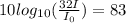

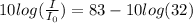
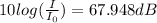
Therefore the sound intensity due to one person is 67.948dB