Question

What will the density be if the radius of the sphere is halved

Answer 1

Density would be 8 times.

Explanation:

Let r represent radius of original sphere.

We are asked to determine the density of a sphere, when its radius is halved.

We know that density is inversely proportional to cube of radius .

`\text{Density}=(1)/(r^3)`

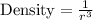
When radius is halved, so new radius would be
`(r)/(2)`.

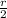Now density would be:

`\text{New density}=(1)/(((r)/(2))^3)`

`\text{New density}=(1)/((r^3)/(2^3))`

`\text{New density}=(1)/((r^3)/(8))`

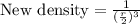
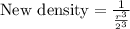
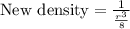
Using property
`(a)/((b)/(c))=(a\cdot c)/(b)`, we will get:

`\text{New density}=(1*8)/(r^3)`

`\text{New density}=(8)/(r^3)`

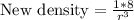
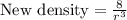
We can see that new density is 8 times the original density. Therefore, the density would be 8 times if the radius of the sphere is halved.