Question

Scores on a final exam taken by 1200 students have a bell shaped distribution with mean=72 and standard deviation=9

a. median score?

b.scores between 63 and 81

c. scores between 72 and 90

d. below 54

Answer 1

a. 72

b. 816

c. 570

d. 30

Explanation:

Given the graph is a bell - shaped curve. So, we understand that this is a normal distribution and that the bell - shaped curve is a symmetric curve.

Please refer the figure for a better understanding.

a. In a normal distribution, Mean = Median = Mode

Therefore, Median = Mean = 72

b. We have to know that 68% of the values are within the first standard deviation of the mean.

i.e., 68% values are between Mean
`$ \pm $` Standard Deviation (SD).

Scores between 63 and 81 :

Note that 72 - 9 = 63 and

72 + 9 = 81

This implies scores between 63 and 81 constitute 68% of the values, 34% each, since the curve is symmetric.

Now, Scores between 63 and 81 =
`$ (68)/(100) * 1200 $`

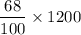
= 68 X 12 = 816.

That means 816 students have scored between 63 and 81.

c. We have to know that 95% of the values lie between second Standard Deviation of the mean.

i.e., 95% values are between Mean
`$ \pm $` 2(SD).

Note that 90 = 72 + 2(9) = 72 + 18

Also, 54 = 63 - 18.

Scores between 54 and 90 totally constitute 95% of the values. So, Scores between 72 and 90 should amount to
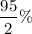`$ (95)/(2) \% $` of the values.

Therefore, Scores between 72 and 90 =
`$ (95)/(2(100)) * 1200 = (95)/(200) * 1200  $`

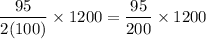
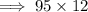`$ \implies 95 * 12 $` = 570.

That is a total of 570 students scored between 72 and 90.

d. We have to know that 5 % of the values lie on the thirst standard Deviation of the mean.

In this case, 5 % of the values lie between below 54 and above 90.

Since, we are asked to find scores below 54. It should be 2.5% of the values.

So, Scores below 54 =
`$ (2.5)/(100) * 1200 $`

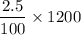
= 2.5 X 12 = 30.

That is, 30 students have scored below 54.