To solve this problem it is necessary to apply the concepts related to thermal transfer given by the thermodynamic definition of heat as a function of mass, specific heat and temperature change.
Mathematically this is equivalent to
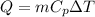
Where
m = mass
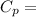 Specific Heat
Specific Heat
 Change at temperature
Change at temperature
In mass terms (KJ / g) this can be expressed as

Our values are given as
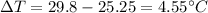
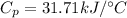
Replacing,

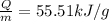
Therefore the heat of combustion per gram on the material is 55.51KJ/g