Question

Write the explicit formula for the geometric sequence given the following: a4 = 12, r = 2

Answer 1

The explicit formula is :
`a_n =  (1.5)(2)^((n-1))`

Explanation:

Here, in the given GP sequence,

a(4) = 12, r = 2

Now, the general term in a geometric sequence is given as:

`a_n =  ar^((n-1))`

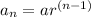
Now, here substituting the value of n = 4 , we get:

`a_4 =  ar^((\\4-1))\\\implies a_4  = ar^3  = a(2)^3  = a *  8 \\\implies a _4  = 8 a\\\implies 12 = 8 a\\\implies a = 12/8 = 1.5`

So, here the first term (a) in the sequence = 1.5

So, the explicit formula is given as :

`a_n =  (1.5)(2)^((n-1))`

Hence, the explicit formula is :
`a_n =  (1.5)(2)^((n-1))`