Question

Show your work ...............

Answer 1

Image:

W"(-3,-2), X"(-1,-5), Y"(0,-4)

Explanation:

Given points:

W(2,0) , X(4,3), Y(5,2)

Transformation sequence:

`(x,y)\rightarrow(x,-y)\rightarrow(x-5,y-2)`

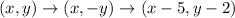
To find image after the transformation.

First transformation:

`(x,y)\rightarrow(x,-y)`

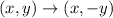
The given transformation shows reflection on x-axis.

`W(2,0)\rightarrow W'(2,0)`

`X(4,3)\rightarrow X'(4,-3)`

`Y(5,2)\rightarrow Y'(5,-2)`

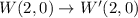
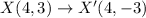
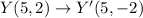
Second transformation:

`(x,y)\rightarrow(x-5,y-2)`

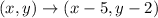
The given transformation shows translation of 5 units to the left and 2 units down.

`W'(2,0)\rightarrow W''(2-5,0-2)=(-3,-2)`

`X'(4,-3)\rightarrow X`

`Y'(5,-2)\rightarrow Y`

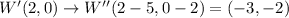
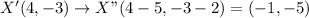
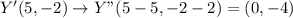
Image:

W"(-3,-2), X"(-1,-5), Y"(0,-4)