Question

Tell whether the lines y=-4x+3 and -2x+8y=5 are parallel, perpendicular, or neither.

Answer 1

The lines are perpendicular to each other.

Explanation:

Given equations of lines:

1.
`y=-4x+3`

2.
`-2x+8y=5`

Writing equation both equations in slope-intercept form which is

`y=mx+b`

where
`m` represents slope and
`b` represents y-intercept.

1.
`y=-4x+3`

This is already in slope-intercept form.

The slope of the line

`m_1=-4`

2.
`-2x+8y=5`

Adding
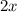`2x` both sides.

`-2x+8y+2x=2x+5`

`8y=2x+5`

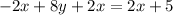
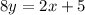
Dividing both sides by 8.

`(8y)/(8)=(2x+5)/(8)`

`y=(2x+5)/(8)`

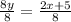
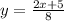
Splitting denominators.

`y=(2x)/(8)+(5)/(8)`

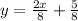
Simplifying fraction.

`y=(1)/(4)x+(5)/(8)`

So, for the line the slope is.

`m_2=(1)/(4)`

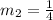
A) Checking for parallel.

For parallel lines the slopes of the line are equal.

Since
`m_1\\eq m_2`

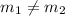
So, lines are not parallel.

B) Checking for perpendicular.

For perpendicular line the slopes of the line are related as:

`m_1* m_2=-1`

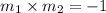
Finding the product of the slopes to check weather it equals -1.

`-4*(1)/(4)`

⇒
`-1`

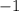
The condition for perpendicular lines is satisfied as the product of the slopes =-1

Hence, the lines are perpendicular to each other.