Question

You want to build a 95% confidence interval for the average IQ of all statistics instructors.

You randomly select 20 statistics instructors and measure their IQ's. You get a sample average of 143. It is known that the population of IQ's is normally distributed with a population standard deviation of 16.

What is the upper confidence limit (UCL) of you confidence interval?

Round your answer to the nearest integer.

Answer 1

Upper limit 150

Lower bond 136

Explanation:

Hello!

The study variable is:

X: measurement of IQ of a statistic instructor.

This variable has a normal distribution:

X~N(μ; σ²)

And the population standard deviation is known σ= 16

You need to construct a confidence interval for the population mean, for this, since the variable has a normal distribution and the population variance is known, the statistic to use is the standard normal

Z= X[bar] - μ ~N(0;1)

σ/√n

The formula for the interval is:

X[bar] ±
`Z_(1-\alpha /2)` *
`((S)/(√(n) ) )`

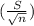
Where

X[bar] is the sample mean

`Z_(1-\alpha /2)` is the value under the Z distribution for the corresponding confidence level.

S is the population standard deviation. (should be sigma but it doesn't recognize the symbol)

`Z_(1-\alpha /2) = Z_(0.975) = 1.96`

[143 ± 1.96 *
`((16)/(√(20) ) )`]

[135,988; 150. 012] ≅ [136; 150]

I hope it helps!