Question

Suppose certain coins have weights that are normally distributed with a mean of 5.566 g and a standard deviation of 0.062 g. A vending machine is configured to accept those coins with weights between 5.496 g and 5.636 g.

A. If 270 different coins are inserted in the vending machine, what is the expected number of rejected coins?B. If 270 different coins are inserted in the vending machine, what is the probability that the mean falls between the limits of 5.496 g and 5.636.

Answer 1

a) 70 coins are expected to be rejected if 270 coins are inserted.

b) If 270 different coins are inserted in the vending machine, the probability that the mean falls between the limits of 5.496 g and 5.636 is 74%

Explanation:

If certain coins have weights that are normally distributed with a mean of 5.566 g and a standard deviation of 0.062 g. and vending machine is configured to accept those coins with weights between 5.496 g and 5.636 g

then margin of error (ME) for the mean weight of coin is estimated as

ME= 5.566 - 5.496 = 5.636 - 5.566 = 0.07

Confidence level for the margin of error can be calculated using the equation:

z=
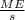`(ME)/(s)` where

• z is the corresponding statistic of the confidence level
• ME is the margin of error (0.07)
• s is the standard deviation (0.062)

Then z=
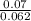`(0.07)/(0.062)` ≈ 1.13

Corresponding two tailed confidence level for z is 74%

Thus

a) If 270 different coins are inserted in the vending machine

then 270 × (100%-74%) ≈ 70 is the expected number of rejected coins.

b) the probability that the mean falls between the limits of 5.496 g and 5.636 is 74%