Question

The standard deviation of political tolerance (measured on a 10 point scale) in a sample of 27 adults is 3.6. The sample mean is 7.4. Test the null hypothesis that this sample is drawn from a population with a mean of 8.5 on the political tolerance measure (at α= .01).

Answer 1

We can conclude that sample is drawn from a population with a mean of 8.5 on the political tolerance measure at α= .01 (accept the null hypothesis)

Explanation:

`H_(0)`: mu=8.5

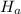`H_(a)`: mu≠8.5

Test statistic can be calculated using the equation:

t=
`(X-M)/((s)/(√(N) ) )` where

• X is the sample mean (7.4)

• M is the population mean on political tolerance (8.5)

• s is the standard deviation (3.6)

• N is the sample size (27)

Then t =
`(7.4-8.5)/((3.6)/(√(27) ) )` ≈−1.588

t-critical at α= .01 and 26 degrees of freedom is 2.779

Since |t|=1.588 < 2.779, the result is not significant, we fail to reject the null hypothesis.