Answer:
8(x2 + 2x) = –3
8(x2 + 2x + 1) = –3 + 8
x = –1 Plus or minus StartRoot StartFraction 5 Over 8 EndFraction EndRoot
Explanation:
Solving Quadratic Equations
Sometimes it's preferred to solve quadratic equations without the use of the known quadratic formula solver. One of the most-used methods consists of completing squares and solving for x.
We have the equation

We separate variables from constants
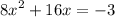
Taking the common factor 8
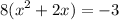
Completing squares in the brackets and balancing the equation in the right side
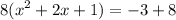
Factoring the perfect square
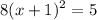
Isolating x
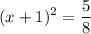
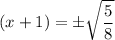
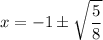
We can clearly see the steps used to solve the quadratic equation are (in order and written like in the question)
8(x2 + 2x) = –3
8(x2 + 2x + 1) = –3 + 8
x = –1 Plus or minus StartRoot StartFraction 5 Over 8 EndFraction EndRoot