Question

You've recently read about a chemical laser that generates a 20.0-cm-diameter, 22.0 MW laser beam. One day, after physics class, you start to wonder if you could use the radiation pressure from this laser beam to launch small payloads into orbit. To see if this might be feasible, you do a quick calculation of the acceleration of a 20.0-cm-diameter, 99.0 kg, perfectly absorbing block. What speed would such a block have if pushed horizontally 100 m along a frictionless track by such a laser?

Answer 1

0.3847 m/s

Step-by-step explanation:

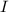`I` = Intensity =
`(P)/(A)=(P)/(\pi r^2)`

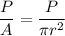
d = Diameter = 20 cm

r = Radius =
`(d)/(2)=(20)/(2)=10\ cm`

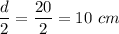
c = Speed of light =
`3* 10^8\ m/s`

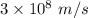
s = Distance = 100 m

P = Power = 22 MW

Pressure due to the laser is given by

`P_r=(I)/(c)\\\Rightarrow P_r=(P)/(Ac)\\\Rightarrow P_r=(P)/(\pi r^2c)\\\Rightarrow P_r=(22* 10^(6))/(\pi 0.1^2* 3* 10^8)\\\Rightarrow P_r=2.33427\ N/m^2`

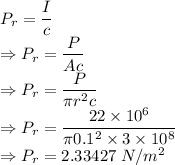
Force is given by

`F=P_rA\\\Rightarrow F=2.33427* \pi 0.1^2\\\Rightarrow F=0.07333\ N`

Acceleration is given by

`a=(F)/(m)\\\Rightarrow a=(0.07333)/(99)\\\Rightarrow a=0.00074\ m/s^2`

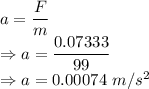
Speed of the block would be

`v=√(2as)\\\Rightarrow v=√(2* 0.00074* 100)\\\Rightarrow v=0.3847\ m/s`

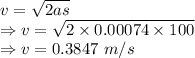
The speed of the block is 0.3847 m/s