Question

A mass of 2000 kg is raised 5.0 m in 10 seconds. What is the power output in horsepower to raise the object?

13
7.5 x 10^6

Answer 1

9800 W

Step-by-step explanation:

Answer 2

The power output in horsepower to raise the object is 13.14 horsepower(Hp).

Step-by-step explanation:

It is known that power required to perform a work is defined as the ratio of energy utilized to do that work per unit time. So, we can write power as the ratio energy utilized to time taken for completing that work.

Thus,

`Power =\frac{\text { Energy utilized to do a work }}{\text { Time taken to complete a work }}`

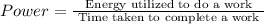
As we known that energy utilized to complete a work will be equal to the work done on the object. Thus,

`Energy utilized = Work done =Weight * displacement`

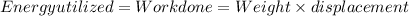
So,

`Power =\frac{\text {Weight} * \text { Displacement }}{\text { Time taken }}`

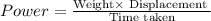
As it is given in the question that mass of the object is 2000 kg and the object is displaced to 5 m from the ground. So the displacement will be 5 m and the weight of the object can be determined by multiplying the mass with acceleration due to gravity.

Thus, the power formulation can be written as

`Power =(m * a * d)/(t)`

`Power =(2000 * 9.8 * 5)/(10)=9800 \mathrm{J} / \mathrm{s}=9800 \mathrm{W}`

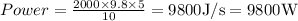
But, we need to find in horsepower unit. So, the conversion between watt and horsepower unit is

1 horsepower (hp) = 745.7 watts

Thus,

`Power =9800 watts =745.7$ horsepower unit`

`Power =(9800)/(745.7)=13.14 horsepower unit`

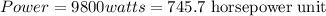
So, the power output in horsepower unit is 13.14 horsepower (Hp).