Question

1) After a dilation, (-60, 15) is the image of (-12, 3). What are the coordinates of the image of (-2,-7) after the same dilation?

a) k = 5; (-10, -35)
b) k = 5; (-7, -2)
c) k = 1/5; (-2/5,-7/5)
d) k = 1/5; (-5/2,-5/7)

Answer 1

a) k = 5; (-10, -35)

Explanation:

Given:

Co-ordinates:

Pre-Image = (-12,3)

After dilation

Image = (-60,15)

The dilation about the origin can be given as :

Pre-Image
`(x,y)\rightarrow Image(kx,ky)`

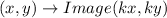
where
`k` represents the scalar factor.

We can find value of
`k` for the given co-ordinates by finding the ratio of
`x` or
`y` co-ordinates of the image and pre-image.

`k=(Image)/(Pre-Image)`

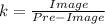
For the given co-ordinates.

Pre-Image = (-12,3)

Image = (-60,15)

The value of
`k=(-60)/(-12)=5`

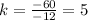
or
`k=(15)/(3)=5`

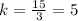
As we get
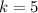`k=5` for both ratios i.e of
`x` and
`y` co-ordinates, so we can say the image has been dilated by a factor of 5 about the origin.

To find the image of (-2,-7), after same dilation, we will multiply the co-ordinates with the scalar factor.

Pre-Image
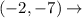`(-2,-7)\rightarrow` Image
`((-2*5),(-7* 5))`

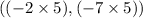
Pre-Image
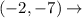`(-2,-7)\rightarrow` Image
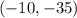`(-10,-35)` (Answer)