Answer:
The value of x is
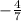
Step by step explanation:
In the question we are given a product that contains two unknown variables, i.e.
 and
and
 . To solve for
. To solve for
 we shall first compute the product between the two brackets. I will show each step in full detail, in order to understand the product computation of such cases (i.e. distributive property).
we shall first compute the product between the two brackets. I will show each step in full detail, in order to understand the product computation of such cases (i.e. distributive property).
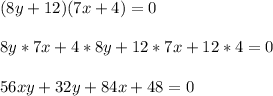
Up to this point we have computed the product and now we have all our terms. Since we want to find the value of
 we will gather together all terms that contain
we will gather together all terms that contain
 (even if they also contain
(even if they also contain
 ) and then do some manipulations and simplifications to obtain our result, as follow:
) and then do some manipulations and simplifications to obtain our result, as follow:
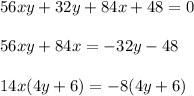
Now we see that on both sides of the equality we have a common term of
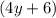 , which we can cancel out from both sides, which leaves us with:
, which we can cancel out from both sides, which leaves us with:
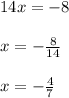
Thus the value of
 is
is
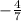 .
.