Question

What is the y-intercept of the line perpendicular to 2x + y + 5 = 0 at (-1 , -3)?

Answer 1

Answer: -2.5

Explanation:

Given that the slope of the first line is
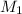`M_(1)` and the slope of the second line is
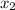`x_(2)` ,if the two lines are perpendicular then
`M_(1)`
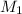
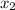`x_(2)` = -1 ,

The line given is 2x + y + 5 =0 , to find the slope of the line , we will need to make y the subject of the formula

2x + y +5 = 0

y = -2x -5

comparing the solution to the equation of line in slope - intercept form , which is given as y = mx + c , where m is the slope and c is the y-intercept. This means that the slope of the given line is -2.

Therefore , the slope of the line perpendicular to this line is given as
`(1)/(2)`. The point given is (-1 , -3 ). Thus , to find the equation of the new line , we will use the formula for finding equation of line in slope-point form , which is given as :

y -
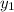`y_(1)` = m ( x -
`x_(1)` )

m =
`(1)/(2)`

`x_(1)` = -1

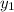`y_(1)` = -3

substituting into the formula , we have

y - ( -3 ) =
`(1)/(2)`( x - {-1} )

y + 3 =
`(1)/(2)`(x + 1)

y + 3 =
`(1)/(2)`x +
`(1)/(2)`

making y the subject of the formula in order to write the equation in slope - intercept form , we have

y =
`(1)/(2)`x +
`(1)/(2)` - 3

y =
`(1)/(2)`x -
`(5)/(2)`

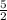
Therefore , the y - intercept is - 2.5