Question

Find y-intercept, x-intercept, vertical asymptote, slant asymptote, the domain and range. PLEASEEEEE 100pts !!!!!!

Answer 1

x=( − 2 + √ 7 , 0 ) , ( − 2 − √ 7 , 0 )

y=( 0 , 1 4 )

Vertical : x = - 4

Oblique :

y = − x/ 3

domain=( − ∞ , − 4 ) ∪ ( − 4 , ∞ )

range=( − ∞ , ∞ ) , y

Answer 2

`\textsf{y-intercept}: \quad \left(0,(1)/(4)\right)`

`\textsf{x-intercepts}: \quad \left(-2+√(7),0\right) \textsf{ and }\left(-2-√(7),0\right)`

`\textsf{vertical asymptote}: \quad x=-4`

`\textsf{slant asymptote}: \quad y=-(1)/(3)x`

`\textsf{domain}: \quad (- \infty, -4) \cup (-4, \infty)`

`\textsf{range}: \quad (- \infty, \infty)`

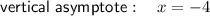
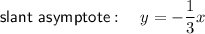
Explanation:

Given function:

`f(x)=(x^2+4x-3)/(-3x-12)`

y-intercept

The y-intercept is the point at which the curve crosses the y-axis.

To find the y-intercept, substitute x = 0 into the function:

`\begin{aligned} \implies f(0)& =((0)^2+4(0)-3)/(-3(0)-12)\\\\ & =(-3)/(-12)\\\\ & = (1)/(4)\end{aligned}`

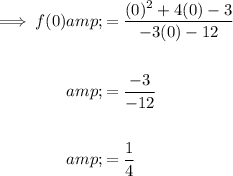
Therefore, the y-intercept is (0, 1/4)

x-intercepts

The x-intercepts are the points where the curve crosses the x-axis.

To find the x-intercepts, set the function to zero and solve for x:

`\begin{aligned} f(x) & = 0\\\\\implies (x^2+4x-3)/(-3x-12) & = 0\\\\x^2+4x-3 & = 0\end{aligned}`

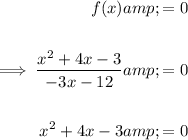
Solve using the quadratic formula:

`x=(-b \pm √(b^2-4ac) )/(2a)\quad\textsf{when }\:ax^2+bx+c=0`

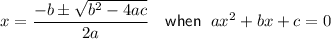
Therefore:

`\implies x=(-4 \pm √(4^2-4(1)(-3)))/(2(1))`

`\implies x=(-4 \pm √(28))/(2)`

`\implies x=(-4 \pm 2√(7))/(2)`

`\implies x=-2\pm√(7)`

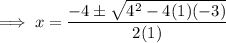
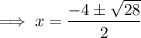
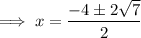
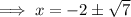
Therefore, the x-intercepts are:

`\left(-2+√(7),0\right) \textsf{ and }\left(-2-√(7),0\right)`

Vertical Asymptote

An asymptote is a line which the curve gets infinitely close to, but never touches.

The vertical asymptote is the value of x that makes the denominator of the function zero.

`\implies -3x-12=0`

`\implies x=4`

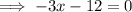
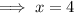
Therefore, the vertical asymptote is x = 4

Slant Asymptote

A slant asymptote occurs when the polynomial in the numerator of a rational function is a higher degree than the polynomial in the denominator.

To find the slant asymptote, divide the numerator by the denominator:

`\large \begin{array}{r}-(1)/(3)x\phantom{)))))}\\-3x-12{\overline{\smash{\big)}\,x^2+4x-3\phantom{)}}}\\\underline{-~\phantom{(}(x^2+4x)\phantom{-))}}\\-3\phantom{)}\end{array}`

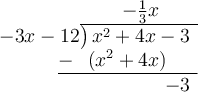
Therefore, the slant asymptote is:

`y=-(1)/(3)x`

Domain

Input values (x-values): (-∞, -4) ∪ (-4, ∞)

Range

Output values (y-values): (-∞, ∞)