Answer:
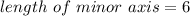
Explanation:
Given:
The given equation is.
 -------------(1)
-------------(1)
We write standard equation of an ellipse
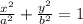 -------(2)
-------(2)
So equation 1 divided by 36 for standard form of an equation
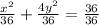
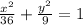
So we compare equation 1 and equation 2.
we get
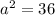 and
and

so
 and
and
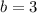
The length of the minor axis is

Here
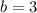 .
.
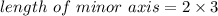
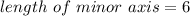
Therefore the length of the minor axis is 6