Answer:
The value of
 is 4.8.
is 4.8.
Explanation:
Given:
The function is given as:
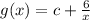
The graph of 'g' passes through the point (5, 6)
The ordered pair (5, 6) represents that at
 , the function's value is 6.
, the function's value is 6.
So,

So, we plug in 5 for 'x' in
 and equate the function to 6. This gives,
and equate the function to 6. This gives,
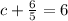
Adding
 both sides, we get:
both sides, we get:
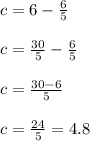
Therefore, the value of 'c' is 4.8.