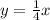Answer:
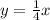
Explanation:
Given equation of line:
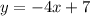
To find the equation of line perpendicular to the line of the given equation and passes through point (8,2).
Applying slope relationship between perpendicular lines.

where
 and
and
 are slopes of perpendicular lines.
are slopes of perpendicular lines.
For the given equation in the form
 the slope
the slope
 can be found by comparing
can be found by comparing
 with standard form.
with standard form.
∴
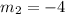
Thus slope of line perpendicular to this line
 would be given as:
would be given as:
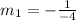
∴
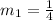
The line passes through point (8,2)
Using point slope form:
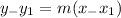
Where
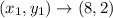 and
and
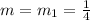
So,
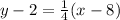
Using distribution.
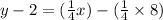
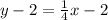
Adding 2 to both sides.
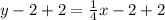
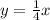
Thus the equation of line in standard form is given by: