Question

| 10. Triangle ABC ~Triangle DEF with AB = 8, BC = 12,

AC = 16, and DE = 12. What is the
perimeter of ADEF?

Answer 1

Perimeter of triangle DEF = 54 units

Explanation:

Given:

Δ ABC is similar to Δ DEF

AB = 8, BC = 12, AC =16 and DE = 12.

Since, the two triangle are similar, their corresponding sides will be in proportion. Therefore,

`(AB)/(DE)=(BC)/(EF)=(AC)/(DF)`

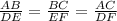
Now, consider the first two ratios.

`(AB)/(DE)=(BC)/(EF)`

Plug in 8 for AB, 12 for BC, 12 for DE and solve for EF. This gives,

`(8)/(12)=(12)/(EF)\\8* EF=12* 12\\8* EF=144\\EF=(144)/(8)=18`

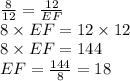
Now, consider the ratio:

`(AB)/(DE)=(AC)/(DF)`

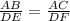
Plug in 8 for AB, 16 for AC, 12 for DE and solve for DF. This gives,

`(8)/(12)=(16)/(DF)\\8* DF=16* 12\\8* DF=192\\DF=(192)/(8)=24`

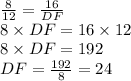
Therefore, the lengths of sides of triangle DEF are:

DE = 12, EF = 18 and DF = 24

Now, perimeter is the sum of all the sides of the triangle. Therefore,

`Perimeter=DE +EF+DF\\Perimeter=12+18+24=54`

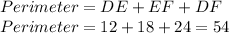
Therefore, the perimeter of the triangle DEF is 54 units.