Question

Ax = 44.4 m and Ay = 25.1 m
Find the magnitude of the
vector.

Answer 1

The magnitude of the vector A is 51 m.

Step-by-step explanation:

Given:

The horizontal component of a vector A is given as:

`A_x=44.4\ m`

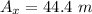
The vertical component of a vector A is given as:

`A_y=25.1\ m`

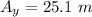
Now, we know that, a vector A can be resolved into two mutually perpendicular components; one along the x axis and the other along the y axis. The magnitude of the vector A can be written as the square root of the sum of the squares of each component.

Therefore, the magnitude of vector A is given as:

`|\overrightarrow A|=\sqrt{A_(x)^2+A_(y)^2}`

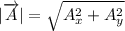
Now, plug in 44.4 for
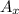`A_x`, 25.1 for
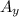`A_y` and solve for the magnitude of A. This gives,

`|\overrightarrow A|=√((44.4)^2+(25.1)^2)\\|\overrightarrow A|=√(1971.36+630.01)\\|\overrightarrow A|=√(2601.37)\\|\overrightarrow A|=51\ m`

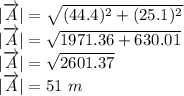
Therefore, the magnitude of the vector A is 51 m.