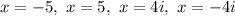Question

Find all the zeros of the equation
-3x^4 + 27x^2 + 1200 = 0

Answer 1

`\displaystyle x=-5,\ x=5,\ x=4i,\ x=-4i`

Explanation:

Biquadratic Equation

It's a fourth-degree equation where the terms of degree 1 and 3 are missing. It can be solved for the variable squared as if it was a second-degree equation, and then take the square root of the results

Our equation is

`\displaystyle -3x^4+27x^2+1200=0`

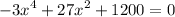
If we call
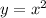`y=x^2`, our equation becomes a second-degree equation

`\displaystyle -3y^2+27y+1200=0`

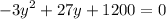
Dividing by -3

`\displaystyle y^2-9y-400=0`

Factoring

`\displaystyle (y-25)(y+16)=0`

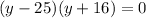
It leads to these solutions

`\displaystyle y=25\ ,\ y=-16`

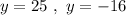
Taking back the change of variable, we have for the first solution

`\displaystyle x^2=25\Rightarrow x=-5,x=5`

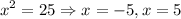
Now for the second solution, we get imaginary (complex) values

`\displaystyle x^2=-16\Rightarrow x=4i,\ x=-4i`

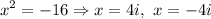
Summarizing, the four solutions for x are

`\displaystyle x=-5,\ x=5,\ x=4i,\ x=-4i`